强化学习（Reinforce Learning）入门例子

强化学习(Reinforce Learning)是机器学习的重要分支之一，这篇博客讲解了强化学习的基本概念，并分析了一个简单的例子，希望让不熟悉强化学习的人能对它有一个直观的体验和基本的认识

• 什么是强化学习？
• 马尔可夫决策过程（Markvo Decision Processes）
  • 策略（Policy）的数学形式
  • 值函数(Value Function)
  • 贝尔曼等式（Bellman Equation）
• 基本算法
  • 值函数迭代法（Value Iteration）算法
  • 策略迭代（Policy Iteration）算法
• 例子: 倒立摆问题（The Inverted Pendulum）
  • 理论分析
  • 概率转移函数简单估计方法
  • 代码实现
• 参考资料

什么是强化学习？

假设我们有一个位于陌生环境的机器人（agent在这里翻译成机器人并不准确，但比较容易理解），这个机器人可以通过和环境交互从而得到一些奖励，在交互过程中，通过强化学习算法，机器人会不断改进他的动作使奖励的总和最大化。举例来说，这个场景也许是机器人完全自主地玩游戏以获取高分，也许是电脑控制的自动驾驶汽车，当电脑正确的玩游戏或安全快速驾驶时，就可以获取高分奖励。

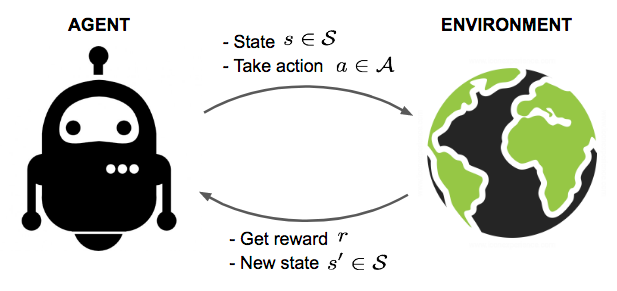
强化学习算法会通过一些前期的测试，让机器人和环境进行简单的交互并收集环境的反馈（奖励），进而学习到一个最优的动作策略，按照这个最优的策略行动，机器人能够很好的适应这个陌生的环境，并且取得最高的奖励。

马尔可夫决策过程（Markvo Decision Processes）

几乎所有的强化学习问题都可以被描述为马尔科夫决策过程（MDPs），一个马尔科夫决策过程由五部分组成：

• $\mathcal{S}$：状态空间（a set of states），所有状态的集合，例如自动驾驶汽车的例子里，汽车可能出现的所有地点的集合组成这个状态空间
• $\mathcal{A}$：动作空间（a set of actions），所有可以采取动作的集合，例如自动驾驶汽车例子中，汽车所有可以执行动作（方向盘，刹车，加速）的集合组成这个操作空间
• $\mathcal{P}_{sa}$：状态转移概率（state transition probabilities），简单来说，$\mathcal{P}_{sa}$描述当采取操作a后，机器人过滤到状态s的概率
• $\gamma\in[0, 1)$：折扣因子（discount factor）
• $\mathcal{R}:\mathcal{S} \times \mathcal{A}\mapsto \mathbb{R}$：奖励函数(Reward Function)，奖励函数与当前所处的状态和采取的动作有关，也可能仅仅与所处状态有关

因此一个马尔科夫过程可以写成$(\mathcal{S, A}, \{\mathcal{P}_{sa}\},\gamma,\mathcal{R})$

一个动态的MDP过程如下：我们从某一个状态$\mathcal{s}_0$开始，采取了某个动作$\mathcal{a}_{0}\in\mathcal{A}$，之后随机过渡到新的状态$\mathcal{s}_1$，${\mathcal{s}_1}$的概率分布是$\mathcal{P}_{\mathcal{s}_0\mathcal{a}_0}$。然后，我们选择另一个动作$\mathcal{a}_{1}$，然后过渡到新的状态$\mathcal{s}_{2} \sim \mathcal{P}_{\mathcal{s}_1\mathcal{a}_1}$。然后在选择新的动作$\mathcal{a}_2$，如此类推……这个过程可以表示如下：

$$\mathcal{s}_0 \xrightarrow{a_0} \mathcal{s}_1 \xrightarrow{a_1} \mathcal{s}_2 \xrightarrow{a_2} s_3 \xrightarrow{a_3} ...$$

策略（Policy）的数学形式

机器人在环境中的动作是由它的策略（Policy）决定的，一个策略在数学上是一个函数，这个函数是状态空间（$\mathcal{S}$）到动作空间（$\mathcal{A}$）的影射，也就是给定一个状态s，根据策略，我们得到下一步采取的动作a，显然策略函数有好有坏，强化学习的目的就是找到一个最优的策略。策略函数，写成数学的形式如下：

$$\pi : \mathcal{S} \mapsto \mathcal{A} \\ a = \pi(s)$$

值函数(Value Function)

当机器人处在一个状态或者采取了一个动作，如何衡量这个状态或者动作的好坏呢？答案是值函数，值函数通过预计未来奖励总和，定量的衡量当前状态或者动作的优劣，公式如下：

$$V = R_0 + \gamma R_1 + \gamma ^2R_2 + \gamma ^3R_3 + ....$$

公式中的$\gamma$就是折扣因子（discount factor），且$0 \leq \gamma \lt 1$，引入这个折扣因子的原因有：

• 未来奖励有很高的不确定性，因此降低未来的奖励是合理的；
• 将来的奖励并不能提供马上的好处；
• 提供了数学上的便利：在折扣因子的作用下，很远的未来的奖励约等于0，可以不考虑

因为状态之间的过渡不是确定的，而是一个根据状态转移概率$\mathcal{P}_{sa}$的随机行为，因此值函数在数学上自然写成期望的形式，表示一个根据概率估计出来的最有可能的值，如下：

$$V = E[R_0 + \gamma R_1 + \gamma ^2R_2 + \gamma ^3R_3 + ....]$$

贝尔曼等式（Bellman Equation）

前面提到过，奖励函数与状态有关，因此奖励函数一般表示为$\mathcal{R}(s)$，带入上面值函数，有：

$$\begin{align} V(s_0) & = E[R(s_0) + \gamma R(s_1) + \gamma ^2R(s_2) + \gamma ^3R(s_3) + ....] \\ & = E[R(s_0)] + \gamma E[R(s_1) + \gamma R(s_2) + \gamma ^2R(s_3)] \\ & = R(s_0) + \gamma V(s_1) \end{align}$$

上述的等式被称为贝尔曼等式，它描述了当前的值函数和执行下一个动作后值函数的关系。

机器人在环境中的执行的下一个动作由策略决定，下面我们结合前面介绍的策略来看看贝尔曼等式

假如我们执行的是一个固定的策略$\pi$，在这个策略下，初始状态$s_0$采取的第一个动作$a_0 = \pi(s_0)$，采取动作后过渡到$s_1$，$s_1$可能是状态空间的任意状态，过渡到各个状态的可能性由状态转移函数$\mathcal{P}_{sa}$决定，因此我们用概率上期望的形式表示我们对采取动作后，下一个状态值函数的估计，如下

$$假设状态空间\mathcal{S} = \{S_a, S_b, S_c, S_d, ...\} 则 \\ \begin{align} V(s_1) & = \mathcal{P}_{s_0a_0}(S_a)V(S_a) + \mathcal{P}_{s_0a_0}(S_b) + \mathcal{P}_{s_0a_0}(S_c) + ... \\ & = \sum_{s^\prime \in \mathcal{S}}\mathcal{P}_{s_0a_0}(s^\prime) \\ & = \sum_{s^\prime \in \mathcal{S}}\mathcal{P}_{s_0\pi(s_0)}(s^\prime) \end{align}$$

所以贝尔曼等式可以写成

$$V(s_0) = R(s_0) + \gamma\sum_{s^\prime \in \mathcal{S}}\mathcal{P}_{s_0\pi(s_0)}(s^\prime)$$

基本算法

强化学习的目的是为了找出最优的行动策略，最优的行动策略下能够取得最大的值函数，在状态空间的状态个数有限，动作空间的动作有限的情况下，有以下两个基本算法得到最优策略

值函数迭代法（Value Iteration）算法

1. 初始化状态空间中所有状态的值函数为0
2. 重复以下的更新， 直到收敛

for every state $s \in \mathcal{S}$ :

更新 $V(s) := R(s) + max_{a \in \mathcal{A}}\gamma\sum_{s^\prime \in \mathcal{S}}\mathcal{P}_{sa}(s^\prime)$

end for

算法的过程分两步

• 第一步是初始化
• 第二步是一个嵌套的循环，逐步接近最优值函数的过程。内层for循环根据贝尔曼等式依次更新各个状态的值函数，取得当前状态下的最优值函数，外层循环不断的调用内层for循环，直到收敛到达全局最优。

算法第二步的两个小细节

• 收敛判断条件是：值函数达到最优值，一次内层for循环更新后，几乎不再改变
• 内层for循环更新公式的含义是，选择当前能够取得最大值函数的动作a，用当前能够得到的最大值更新值函数

在第二步for循环更新值函数时，有两种更新方式都是可行的

• 同步更新：每计算出一个状态s的值函数后，立刻更新他的值函数v(s)，该次for循环后面其他元素更新需要用到v(s)时，用这个更新后的值
• 异步更新：每计算出一个状态s的值函数后，不立刻更新他的值函数v(s)，而是等for循环计算出所有状态新的值函数后，在统一更新

策略迭代（Policy Iteration）算法

1. 随机初始化策略$\pi$，随机初始化各个状态的值函数为一个很小的值
2. 重复以下的更新，直到收敛
   2.1 for every state $s \in \mathcal{S}$
   更新$\pi (s) := arg max_{a \in \mathcal{A}}\gamma\sum_{s^\prime \in \mathcal{S}}\mathcal{P}_{sa}(s^\prime)$
   end for
   2.2 根据当前策略更新值函数$V := V^\pi$

算法的过程分两步

• 第一步是初始化
• 第二步是一个嵌套的循环，逐步接近最优策略的过程。内层for循环又分为两步，2.1 是值函数固定的情况下，根据贝尔曼等式得到当前最优的策略，2.2是策略函数固定的情况下，计算当前的值函数，外层循环不断的调用内层for循环，直到收敛到达全局最优。

例子: 倒立摆问题（The Inverted Pendulum）

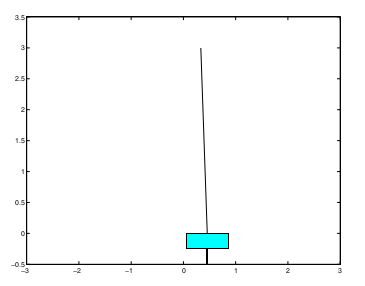
理论分析

如上图所示一个细杆子通过一个自由活动的铰链连在一个小车上，车子通过前后运动，保持杆子尽可能的垂直于地面，我们的目标就是通过强化学习学习一个控制小车运动的策略，达到控制杆子不倒的目标。

我们用马尔科夫模型来分析这个问题

• 状态空间
  车和杆子在任何时刻的状态可以由4个参数表示：车的位置$x$，车的速度$\dot x$，杆子和水平面的夹角$\theta$，杆子的角速度$\dot \theta$，那么状态是一个四维向量（$x$, $\dot x$, $\theta$, $\dot \theta$）
• 动作空间
  车子只能前后运动，因此动作空间有：前进和后退
• 状态转移函数
  未知，需要通过前期实验学习得到
• 折扣因子
  这是一个经验值，这个例子里用的是0.995
• 奖励函数
  当控制失败，奖励函数等于-1，其他情况奖励函数都等于0。控制失败有两种情况：1. $\theta$大于一定角度，即杆子即将落地；2. $x$的绝对值大于一定值，即我们认为这个例子中，车子的运动范围有限制

上述状态空间和状态转移函数需要在详细解释一下

• 状态空间的离散化
  离散化前状态是一个四维向量，且每一维都是连续的，离散化后，小车的状态用一个整数表示，且该整数范围是1到163，这样做的目的是简化处理。这个离散化只是细节，不是强化学习的重点，不在细讲,想弄明白原理，可以参考后面给出的源代码。
• 学习状态转移函数
  在现实的马尔科夫模型中，状态转移函数未知是一种常见情况，在这种情况下，我们可以通过前期的实验估计一个合理的值出来

概率转移函数简单估计方法

假设我们进行了N次倒立摆的控制实验，记录的实验结果如下：

$$s_0^{(1)} \xrightarrow{a_0^{(1)}} s_1^{(1)} \xrightarrow{a_1^{(1)}} s_2^{(1)} \xrightarrow{a_2^{(1)}} ... \\ s_0^{(2)} \xrightarrow{a_0^{(2)}} s_1^{(2)} \xrightarrow{a_1^{(2)}} s_2^{(2)} \xrightarrow{a_2^{(2)}} ... \\ s_0^{(3)} \xrightarrow{a_0^{(3)}} s_1^{(3)} \xrightarrow{a_1^{(3)}} s_2^{(3)} \xrightarrow{a_2^{(3)}} ... \\ ...$$

这里 $s_i^{(j)}$表示第j次实验中第i步的状态，$a_i^{(j)}$表示对应状态下采取的动作，有了以上的N次实验后，那么我们可以估计出状态转移函数为：

$$\mathcal{P}_{sa}(s^\prime) = \frac{小车在状态s，采取动作a，过渡到到状态s^\prime的次数}{小车在状态s，采取动作a的总次数}$$

然而这个公式并不完美:

1. 如果分母为0那么公式在数学上无意义
2. 如果分子为0，那么概率也为0，但实际中做的实验次数有限，直接等于0过于武断

因此，我们可以需要修正这个公式。先用数学符号定义下面的一些量，

$$N(s-a-s^\prime) : 小车在状态s，采取动作a，过渡到状态s^\prime 的次数 \\ N(s-a-all)：小车在状态s，采取动作a的总次数 \\ N(never-reach-state)：小车在状态s，采取动作a，没有过渡到的状态数目$$

用上述记号，上面的公式可以写成

$$\mathcal{P}_{sa}(s^\prime) = \frac{N(s-a-s^\prime)}{N(s-a-all)}$$

修正后的公式为：

$$\mathcal{P}_{sa}(s^\prime) = \begin{cases} \frac{N(s-a-s^\prime)}{N(s-a-all) + N(never-reach-state)}, & \text{如果状态s采取动作a后，至少过渡到状态$s^\prime$一次} \\ \frac{1}{N(s-a-all) + N(never-reach-state)}, & \text{如果状态s采取动作a后，从未过渡到$s^\prime$} \end{cases}$$

我们用一个简单的例子说明修正后的公式的含义
假设状态空间$\mathcal{S} = \{s_0, s_1, s_2\}$，动作空间$\mathcal{A} = \{ a_0, a_1\}$，我们在实验观察到，小车在状态$s_0$下采取动作$a_0$一共4次(即$N(s_0-a_0) = 4$)，采取动作后，过渡到$s_1$3次（$N(s_0-a_0-s_1) = 3$），保持$s_0$状态1次（$N(s_0-a_0-s_0) = 1$），一次都未到达的状态有$s_2$（N(never-reach-state) = 1），根据修正后的公式，我们可以得到如下转移概率：

$$\mathcal{P}_{s_0a_0}(s_0) = \frac{1}{4 + 1} = 0.2 \\ \mathcal{P}_{s_0a_0}(s_1) = \frac{3}{4 + 1} = 0.6 \\ \mathcal{P}_{s_0a_0}(s_0) = \frac{1}{4 + 1} = 0.2 \\$$

代码实现

可以查看我自己实现的源代码

参考资料

• Lilian Weng. A (Long) Peek into Reinforcement Learning